

Abstract:
We present a general computational framework to locally characterize any shape space of meshes implicitly prescribed by a collection of non-linear constraints. We computationally access such manifolds, typically of high dimension and co-dimension, through first and second order approximants, namely tangent spaces and quadratically parameterized osculant surfaces. Exploration and navigation of desirable subspaces of the shape space with regard to application specific quality measures are enabled using approximants that are intrinsic to the underlying manifold and directly computable in the parameter space of the osculant surface. We demonstrate our framework on shape spaces of planar quad (PQ) meshes, where each mesh face is constrained to be (nearly) planar, and circular meshes, where each face has a circumcircle. We evaluate our framework for navigation and design exploration on a variety of inputs, while keeping context specific properties such as fairness, proximity to a reference surface, etc.
Results:
 |
|||
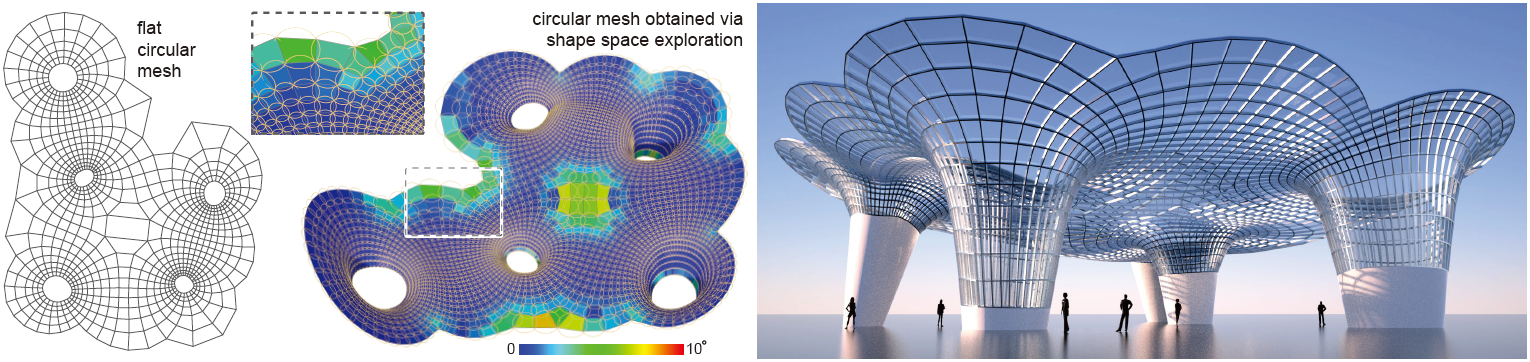
| Starting from a single input mesh along with a set of non-linear constraints, our geometric framework allows local characterization, navigation, and exploration of the corresponding shape space. The figure shows a sample design (right) created using our method, starting from a flat circular mesh (left). | |||
 |
|||
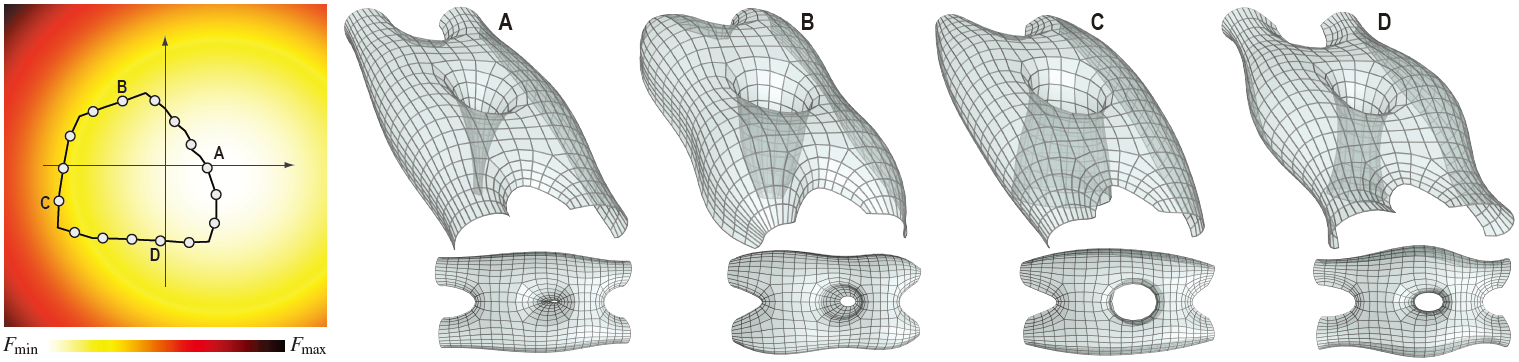
| Spectral analysis of the intrinsic Hessian of energy functions helps to identify good meshes in the neighborhood of an input PQ mesh. The user can interactively navigate a parameter plane T2, while we show the corresponding meshes (points on the osculant). The boundary of maximal planarity (10mm) for each quad face is shown on T2 for guidance. Regular sampling of the boundary polygon provides a quick overview of the exposed design space (see the video below for examples in d = 3). | |||
| |||
 |
|||
| PQ mesh manifold deformation in the presence of an obstacle (in green). Given two user prescribed vertex constraints (in red), mesh B and mesh C are the deformed PQ meshes obtained with and without obstacle constraints, respectively. The obstacle (box) acts as a forbidden region in R^D. | |||
| |||
| |||
 |
|||
| Starting from a single planar quad (PQ) mesh, our geometric framework allows navigation and exploration of the shape space of PQ meshes, enabling easy creation of aesthetic model variants. A global stiffness map informs the user of relative flexibility across the model (reference geometry from Yas Island Marina Hotel, Abu Dhabi, by Asymptote Architecture). | |||
Video:
Acknowledgements:
We thank Daniel Piker for providing the starting "rheotomic" mesh used as the input mesh in Figure 1 and for the starting flat meshes in the upper two rows of Figure 18. We thank Johannes Wallner for his many useful comments and suggestions, Alexander Schiftner, Mathias Hobinger and Michael Eigensatz for their help and valuable comments, and the anonymous reviewers for their feedback. We are grateful to Heinz Schmiedhofer for the final renderings. The work has been partially supported by Austrian Science Fund (FWF) grant P23735-N13 and Austrian Science Promotion Agency (FFG) grant 813391.
Bibtex:
@article{yypm_constrmesh_siga_11,
AUTHOR = "Yong-Liang Yang and Yi-Jun Yang and Helmut Pottmann and Niloy J. Mitra",
TITLE = "Shape Space Exploration of Constrained Meshes",
JOURNAL = "ACM Transactions on Graphics",
VOLUME = "30",
NUMBER = "6",
pages = {124:1--124:12},
articleno = {124},
numpages = {12},
YEAR = "2011",
}
|
|