
Abstract:
We introduce 4PCS, a fast and robust alignment scheme for 3D point sets that uses wide bases, which are known to be resilient to noise and outliers. The algorithm allows registering raw noisy data, possibly contaminated with outliers, without pre-filtering or denoising the data. Further, the method significantly reduces the number of trials required to establish a reliable registration between the underlying surfaces in the presence of noise, without any assumptions about starting alignment. Our method is based on a novel technique to extract all coplanar 4-points sets from a 3D point set that are approximately congruent, under rigid transformation, to a given set of coplanar 4-points. This extraction procedure runs in roughly O(n2+k) time, where n is the number of candidate points and k is the number of reported 4-points sets. In practice, when noise level is low and there is sufficient overlap, using local descriptors the time complexity reduces to O(n+k). We also propose an extension to handle similarity and affine transforms. Our technique achieves an order of magnitude asymptotic acceleration compared to common randomized alignment techniques. We demonstrate the robustness of our algorithm on several sets of multiple range scans with varying degree of noise, outliers, and extent of overlap.
Results:
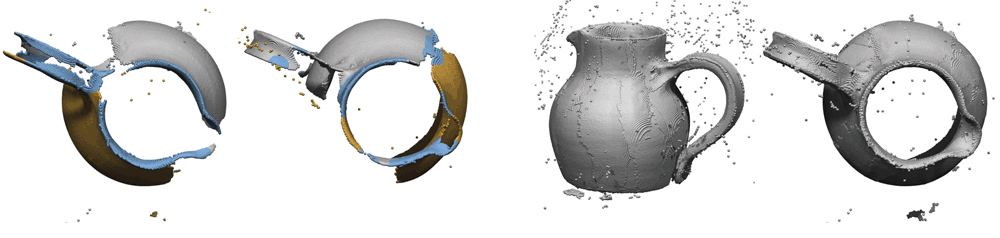 |
|||
| Reconstruction from raw scans using 4-points congruent sets. Reconstruction results from nine input scans of a shinny water jug. Neighboring scans have 40% overlap or less, and required an average of 16 seconds for fully automatic alignment starting from arbitrary initial poses. Pairwise alignment results are robust even with low overlap. Typical pairwise alignments are shown in images on the left-half, where for visualization we roughly mark the overlap regions in blue. The final alignment result (right-half) is obtained without any data smoothing, outlier removal, local ICP refinement, global error distribution, or any assumption about starting alignment. | |||
| |||
 |
|||
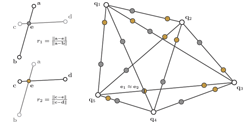
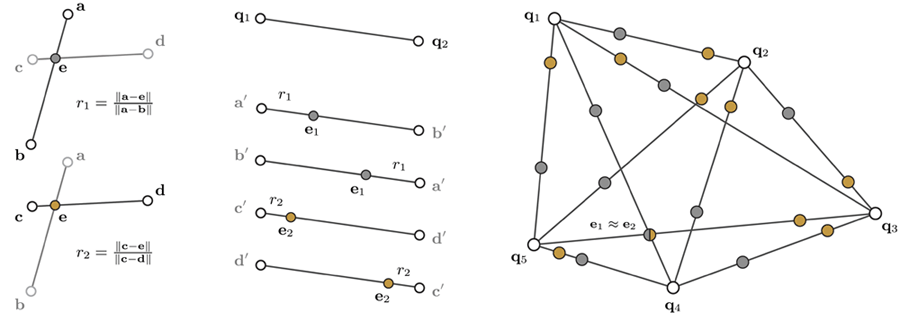
| Extracting affine invariant congruent 4-points. (Left) Given a base B={a,b,c,d} consisting of four (approximately) coplanar points, we extract the two ratios r1 and r2. (Middle) For any point-pair {q1,q2}, there can be two assignments corresponding to {a,b}, and another two assignments corresponding to {c,d} leading to 4 possible intermediate points. These points are computed as e1=q1+r1(q2-q1) and e2=q1+r2(q2-q1). (Right) Now, given a set of coplanar points Q, we want to extract a 4-points set which is congruent to the given base B up to affine transforms. For each pair of points {q1, q2} in Q, we compute four intermediate points as described. For simplicity, we just indicate two points per point-pair in the figure. A set of 4 points is approximately congruent to given B, if e1 ~ e2. In this example, {a,b,c,d} is approximately congruent to {q5, q3, q4, q1}. | |||
| |||
 |
|||
| Aligning building facades. Given two building facades in arbitrary starting poses, 4PCS successfully aligns the scans. This is a challenging case for automatic registration since the scans comprise of noisy data with large flat featureless regions. This example has very few distinct features that can be reliably detected using any local descriptors. (Middle) The result is without any ICP refinement. (Right) We color the error in 4PCS alignment when compared to the final position after ICP refinement. In our scale, we set the length of the bounding box diagonal of the model to unity. Points with error more than 0.01 are marked in blue. Notice that even without ICP refinement our algorithm aligns the scans very reliably. |
Bibtex:
@article{amo_fpcs_sig_08,
AUTHOR = "D. Aiger and N. J. Mitra and D. Cohen-Or",
TITLE = "4-points Congruent Sets for Robust Surface Registration",
JOURNAL = "ACM Transactions on Graphics",
VOLUME = "27",
NUMBER = "3",
PAGES = "\#85, 1-10",
YEAR = "2008",
}
Note:
List of universities and research centers using our algorithm/software can be found here.
|
|