Abstract:

We introduce a computational framework for discovering regular or repeated geometric structures in 3D shapes. We describe and classify possible regular structures and present an effective algorithm for detecting such repeated geometric patterns in point- or meshbased models. Our method assumes no prior knowledge of the geometry or spatial location of the individual elements that define the pattern. Structure discovery is made possible by a careful analysis of pairwise similarity transformations that reveals prominent lattice structures in a suitable model of transformation space. We introduce an optimization method for detecting such uniform grids specifically designed to deal with outliers and missing elements. This yields a robust algorithm that successfully discovers complex regular structures amidst clutter, noise, and missing geometry. The accuracy of the extracted generating transformations is further improved using a novel simultaneous registration method in the spatial domain. We demonstrate the effectiveness of our algorithm on a variety of examples and show applications to compression, model repair, and geometry synthesis.

Results:

Regular structures discovered by our algorithm involve combinations of rotation, translation, and scaling of the repetitive elements.

Schematic illustration of regular structures. The helix and spiral are generated by transformations that combine rotation with translation and scaling, respectively. The images on the right show the three types of commutative 2-parameter groups: rotation and translation along the rotation axis, two independent translations, rotation and scaling with center of scaling on the rotation axis.

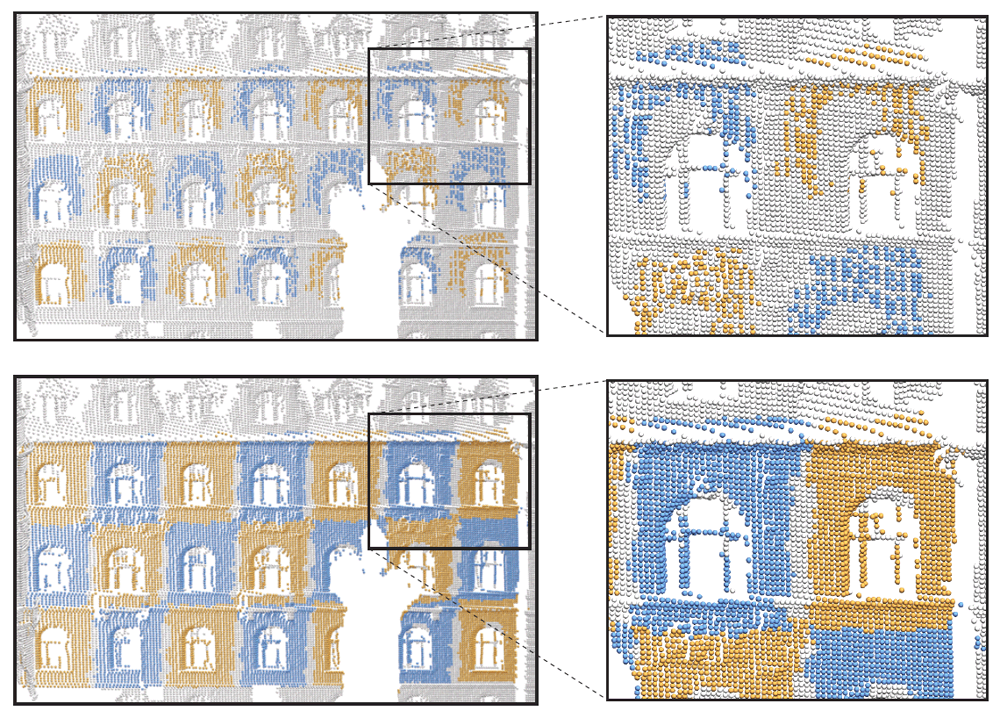
Simultaneous Registration. The colored points show the sample points that are closest to the bottom left element transformed using the estimated group transformations. Aggregation without registration leads to successively stronger misalignments (top row). Our coupled optimization with simultaneous registration significantly improves the accuracy of the generating transformations and allows extracting larger elements (bottom row).

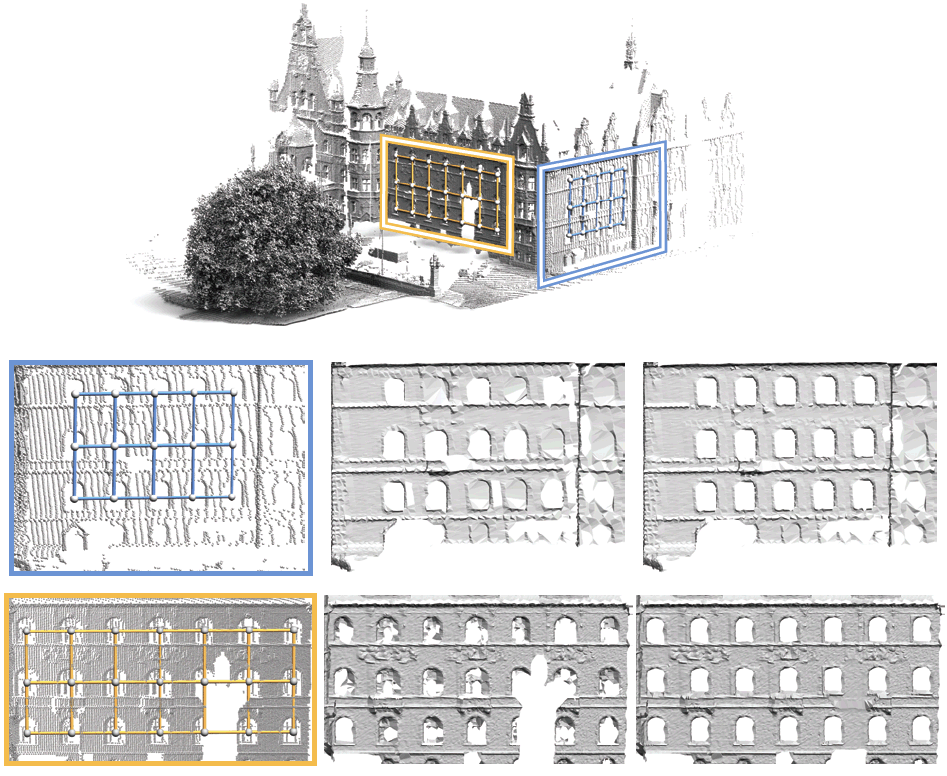
Structure detection and model repair on a complex outdoor scan. Our algorithm fully automatically discovers two translational grids within the acquired point cloud. Standard surface reconstruction yields an incomplete and inconsistent triangulation shown in the middle. The models on the right have been created by augmenting the point set using replicated samples from the representative elements prior to reconstruction.

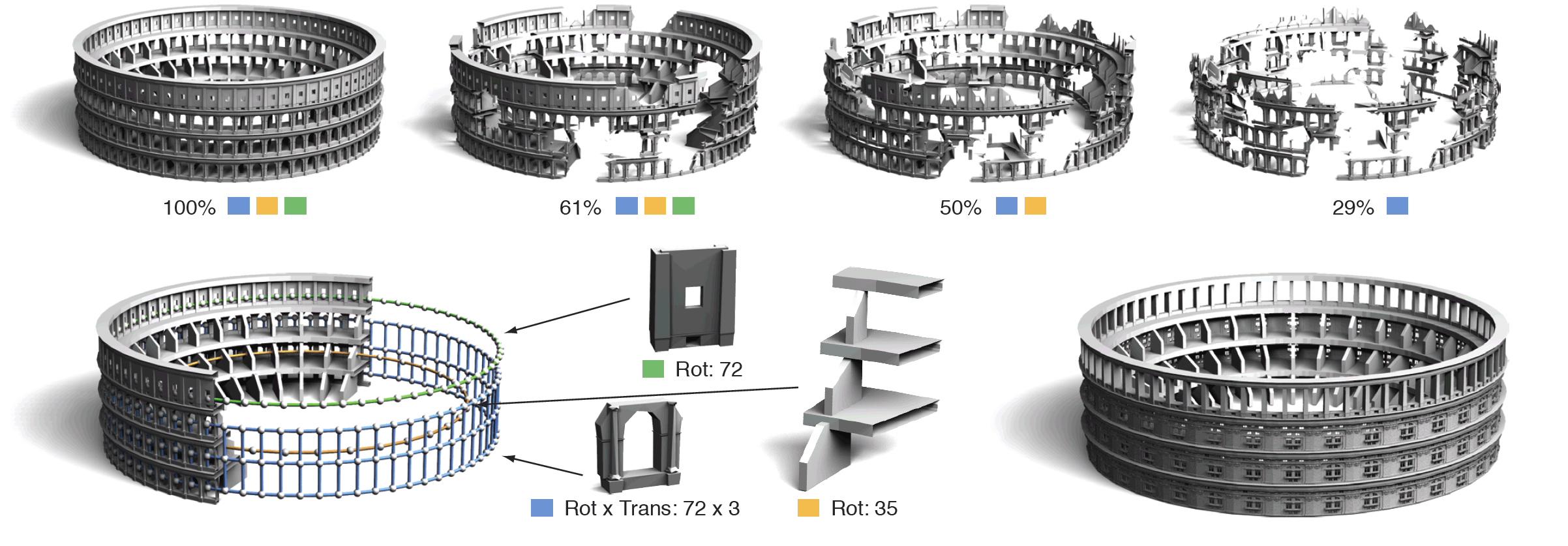Structure discovery and procedural design on a 3D model of an amphitheater. The top row indicates which of the three regular structures can be reconstructed in their entirety when successively removing geometry. The density plots show a section of the distribution of transformations of the structure depicted in blue. The recovered structures are used to procedurally design a new model in the bottom right.

Our method detects multiple 1- and 2-parameter structures. The blue regions denote the representative elements. All structures where detected with 30k samples distributed uniformly across the model, except for the balustrade, for which the rate was increased to 100k.

Model repair and geometry synthesis for a scan of a chambered nautilus shell. From left to right: photograph of original model, input data consisting of 72 registered laser scans, repaired model with additional synthesized elements indicated in orange.

@article{pmwpg_structure_sig_08,
AUTHOR = "M. Pauly and N. J. Mitra and J. Wallner and H. Pottmann and L. Guibas",
TITLE = "Discovering Structural Regularity in {3D} Geometry",
JOURNAL = "ACM Transactions on Graphics",
VOLUME = "27",
NUMBER = "3",
PAGES = "\#43, 1-11",
YEAR = "2008",
}