Abstract:

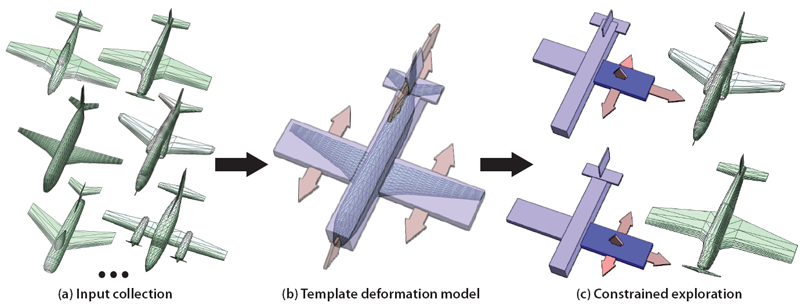
As large public repositories of 3D shapes continue to grow, the amount of shape variability in such collections also increases, both in terms of the number of different classes of shapes, as well as the geometric variability of shapes within each class. While this gives users more choice for shape selection, it can be difficult to explore large collections and understand the range of variations amongst the shapes. Exploration is particularly challenging for public shape repositories, which are often only loosely tagged and contain neither point-based nor part-based correspondences. In this paper, we present a method for discovering and exploring continuous variability in a collection of 3D shapes without correspondences. Our method is based on a novel navigation interface that allows users to explore a collection of related shapes by deforming a base template shape through a set of intuitive deformation controls. We also help the user to select the most meaningful deformations using a novel technique for learning shape variability in terms of deformations of the template. Our technique assumes that the set of shapes lies near a low-dimensional manifold in a certain descriptor space, which allows us to avoid establishing correspondences between shapes, while being rotation and scaling invariant. We present results on several shape collections taken directly from public repositories.

Results:

(Right) Given a collection of unlabeled shapes (top), we compute a descriptor for each shape, embedding them into a canonical domain (bottom). If the shapes were produced by a 1-parameter family of deformations, their descriptors will trace a curve. Moreover, any such family of deformations of a starting shape will produce a curve in the descriptor space (bottom red). By fitting the curve lying most closely to the data, we recover the original deformation.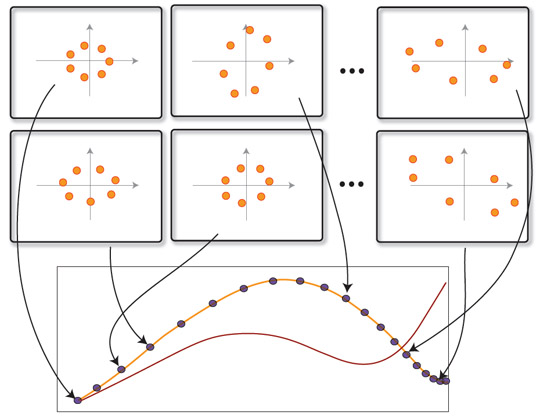

(Bottom) We apply our method to extract templates and deformation models for five classes of shapes (a-e). For eachclass, we show sample template deformations on the left and the corresponding nearest neighbor shapes from the collection on the right. The grey boxes indicate the selected template shape for each dataset. Notice that the learned deformation models capture variations in both the size and position of components. They also encode dependencies between parts, so that, for example, the wings of the airplane move together. In addition, we visualize the principal modes of variation from a dataset with both bicycles and morotcycles (f-g). These modes capture several non-trivial deformations including movement of the wheels along the length and height of the template, and shrinking of the width of the body in the second mode (g). In contrast, a manual deformation of the template is unlikely to include all of the learned deformations (h).

@article{maks_structureDiscovery_sigg11,
AUTHOR = "Maks Ovsjanikov and Wilmot Li and Leonidas Guibas and Niloy J. Mitra ",
TITLE = "Exploration of Continuous Variability in Collections of 3D Shapes",
JOURNAL = "ACM Transactions on Graphics",
VOLUME = "30",
NUMBER = "4",
pages = {33:1--33:10},
articleno = {33},
numpages = {10},
YEAR = "2011",
}