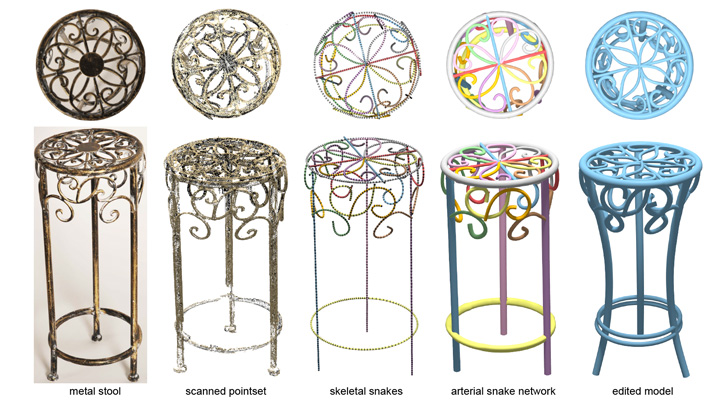

Abstract:
Man-made objects often consist of detailed and interleaving structures, which are created using cane, coils, metal wires, rods, etc. The delicate structures, although manufactured using simple procedures, are challenging to scan and reconstruct. We observe that such structures are inherently 1D, and hence are naturally represented using an arrangement of generating curves. We refer to the resultant surfaces as arterial surfaces. In this paper we approach for analyzing, reconstructing, and manipulating such arterial surfaces. The core of the algorithm is a novel deformable model, called arterial snake, that simultaneously captures the topology and geometry of the arterial objects. The recovered snakes produce a natural decomposition of the raw scans, with the decomposed parts often capturing meaningful object sections. We demonstrate the robustness of our algorithm on a variety of arterial objects corrupted with noise, outliers, and with large parts missing. We present a range of applications including reconstruction, topology repairing, and manipulation of arterial surfaces by directly controlling the underlying curve network and the associated sectional profiles, which are otherwise challenging to perform.
Bibtex:
@INPROCEEDINGS{llzm_arterialSnakes_sigga110,
AUTHOR = "Guo Li and Ligang Liu and Hanlin Zheng and Niloy J. Mitra",
TITLE = "Analysis, Reconstruction and Manipulation using Arterial Snakes",
BOOKTITLE = "ACM Transactions on Graphics",
VOLUME = "29",
NUMBER = "6",
pages = {152:1--152:10},
articleno = {152},
numpages = {10},
YEAR = "2010",
}
Acknowledgements:
Several people helped in generating comparison results namely Junjie Cao and Oscar Au for Laplacian contraction, Misha Kazhdan for Poisson surface reconstruction, Balint Miklos for scale axis computation, Cengiz Oztireli for kernel regression reconstruction, Andrea Tagliasacchi and Richard Hao Zhang for curve skeleton computation, and Guanghua Tan for MPU reconstruction. We thank Min Yue for her help in obtaining the physical models scanned for this paper, Martin Peternell and Johannes Wallner for their help with scanning the models, and Jonathan Balzer for video narration.
|
|